Orbital Elements

An object's orbital elements describe the size, shape, and orientation of the object's orbit, together with the position of the object on its orbit.

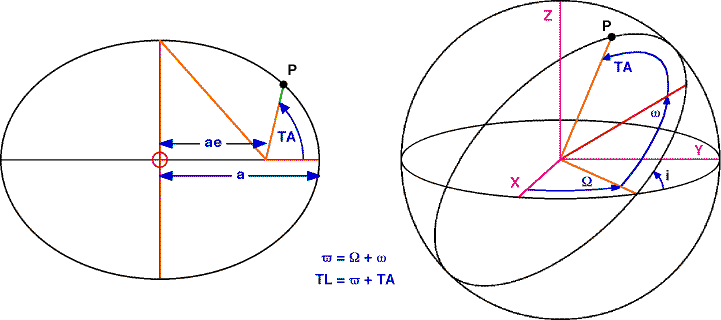
The orbital elements are as follows.

• Semi-Major Axis is the semi-major axis of the orbit, and has the symbol a. This describes the size of the orbit, and for a circular orbit is equal to the radius of the orbit, and for an elliptical orbit is the mean distance of the object from its parent.

  The semi-major axis of the orbit must be a number greater than zero.

• Orbital Eccentricity is the eccentricity of the orbit, and has the symbol e. This describes the shape of the orbit, and is equal to the ratio of the distance of the parent from the center of the orbit to the length of the semi-major axis. A circular orbit has an eccentricity of 0, an elliptical orbit has an eccentricity between 0 and 1, a parabola has an eccentricity of 1, and a hyperbola has an eccentricity greater than 1.

  The eccentricity of the orbit must be a number greater than or equal to zero.

• Orbital Inclination is the inclination of the orbital plane, and has the symbol i. This is one of the three values that describe the orientation of the orbit, and is the angle between the xy-plane and the orbital plane.

  The inclination of the orbital plane may be any number, but will be automatically normalized to lie in the interval [0, π].

• Asc Node Longitude is the longitude of the ascending node, and has the symbol Ω. This is one of the three values that describe the orientation of the orbit, and is the angle between the x-axis and the point where the orbit crosses the xy-plane with an increasing z-coordinate.

  The longitude of the ascending node may be any number, but will be automatically normalized to lie in the interval [0, 2π).

• Peri Longitude is the longitude of the pericenter position, and has the symbol ϖ. This is one of the three values that describe the orientation of the orbit, and is the sum of the ascending node longitude and the peri argument, where the peri argument (one of the other elements) is the angle between the ascending node and the point on the orbit that is closest to the parent.

  The longitude of the pericenter position may be any number, but will be automatically normalized to lie in the interval [0, 2π).

• True Longitude is the longitude of the true position, and has the symbol l (or TL in the above diagram). This describes the position of the object on its orbit, and is the sum of the peri longitude and the true anomaly, where the true anomaly (one of the other elements) is the angle between the point on the orbit that is closest to the parent and the position of the object on its orbit.

  If the orbit is closed (a circle or an ellipse), the longitude of the true position may any number, but will be automatically normalized to lie in the interval [0, 2π). If the orbit is open (a parabola or a hyperbola), the longitude of the true position must lie between the orbit's asymptotes.

Experimenting with the Two Body System sample simulation is a good way to get a better intuitive feel for the orbital elements.

Copyright © 2005-2024, AstroGrav Astronomy Software